NN08 - Performanzanalyse
Videos
Folien
Kurze Übersicht
Performanzmetriken für Klassifizierungsprobleme
Wahrheitsmatrix (engl. Confusion Matrix)
- Gibt eine Übersicht über die Anzahl von richtig und falsch klassifizierten Datenpunkten (bei binärer Klassifizierung)
- Bei Klassifizierungsproblemen mit
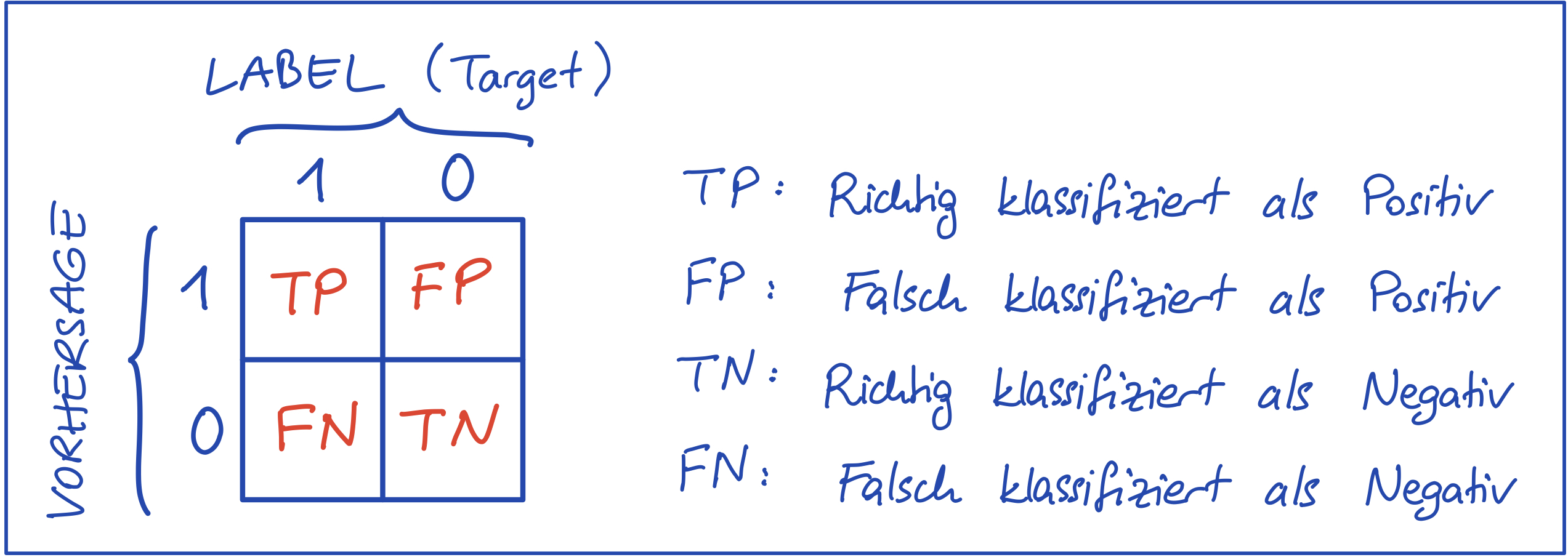
Abbildung 1 - Wahrheitsmatrix bei binärer Klassifizierung
Treffergenauigkeit (engl. Accuracy)
-
Anzahl richtig klassifizierter Datenpunkte, Erfolgsrate (engl. correct rate)
-
Accuracy vermittelt ein falsches Bild des Erfolges bei unausgewogenen Datensätzen
Beispiel:- Klasse 1 hat 10, Klasse 0 hat 990 Beispiele.
- Ein Modell, das immer 0 ausgibt, hat
Precision
- Positive Predictive Value (PPV)
- Antwort auf: Von allen positiven Vorhersagen, wie viele sind richtig?
- Wahrscheinlichkeit, dass ein positiv klassifiziertes Beispiel auch tatsächlich positiv ist.
- Je näher an 1, desto besser.
- Accuracy of positive predictions.
Recall
- True Positive Rate, auch Sensitivität (engl. Sensitivity)
- Antwort auf: Von allen positiven Beispielen, wie viele wurden richtig klassifiziert?
- Wahrscheinlichkeit, dass ein positives Beispiel tatsächlich als solches erkannt wird.
- Je näher an 1, desto besser.
- Accuracy of positive examples.
Precision-Recall Trade-off
- Ein gutes Modell sollte hohe Precision und zugleich hohes Recall haben.
- Man kann die Precision eines Modells beliebig erhöhen (durch das Vergrößern des Schwellenwertes bei der Klassifizierung), jedoch wird dabei der Recall abnehmen.
- Genau so kann man den Recall eines Modells beliebig erhöhen (durch das Verkleinern des Schwellenwertes bei der Klassifizierung), jedoch wird dabei die Precision abnehmen.
- Es gilt ein gutes Trade-off zu finden.
- Eine Zwei-Zahlen-Metrik erschwert den Entscheidungsprozess bei Evaluierung und Modellauswahl.
- Fasst Precision (P) und Recall (R) in einer Metrik zusammen (Harmonisches Mittel von P und R):
- Der
- Je näher an 1, desto besser.
- Sehr kleine P und R Werte ziehen den
Lernziele
- (K2) Performanzmetriken für die Evaluierung von Klassifizierungsmodellen
- (K2) Wahrheitsmatrix (engl. Confusion Matrix)
- (K2) Treffergenauigkeit (engl. Accuracy)
- (K2) Precision (engl. Precision)
- (K2) Recall
- (K2)
- (K3) Berechnung und Deutung von Precision und Recall
- (K3) Berechnung und Deutung des
- (K3) Einsatz bei Evaluierung und Auswahl von Modellen