NN02 - Lineare Regression und Gradientenabstieg
Videos
Folien
Kurze Übersicht
Formalisierung
- Ausgabe
- Die Hypothesenfunktion ist eine gewichtete Summe der Merkmale
- Der Verlust (engl. loss) für einen Datenpunkt
- Die Kosten (engl. cost) sind der durchschnittliche Verlust über alle Datenpunkte:
Der Gradient
- Der Gradientenvektor
- Schlussfolgerung: In die entgegengesetzte Richtung, i.e. in Richtung
- IDEE: Bewege
Der Gradientenabstieg (engl. Gradient Descent)
- Starte mit zufälligen Gewichten
- Berechne den Gradientenvektor im aktuellen Punkt
- Gewichtsaktualisierung: Gehe einen kleinen Schritt in Richtung
- Wiederhole Schritte 2-3, bis das globale Minimum von
Graphische Übersicht
Übungsblätter/Aufgaben
Lernziele
- (K2) Lineare Regression aus Sicht neuronaler Netze: Graphische Darstellung, Vergleich mit Perzeptron
- (K2) Formalisierung
- (K2) Verlust- und Kostenfunktion
- (K2) Gradientenvektor
- (K2) Lernrate
- (K3) Gradientenabstieg
Challenges
Skalierung der Merkmale
Abbildung 1 und Abbildung 2 zeigen die Höhenlinien (Contour Lines) von zwei Kostenfunktionen.
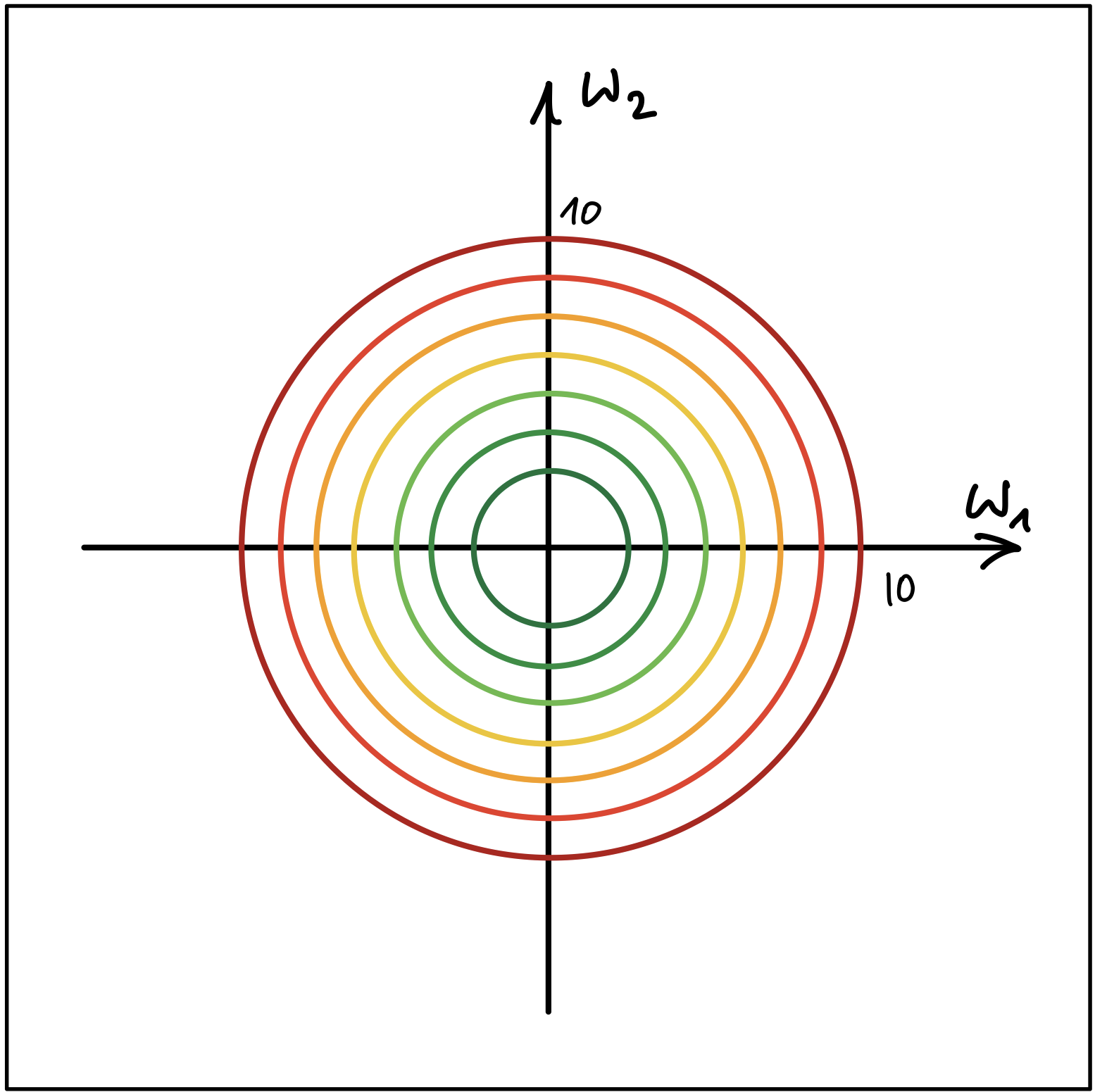
Abbildung 1
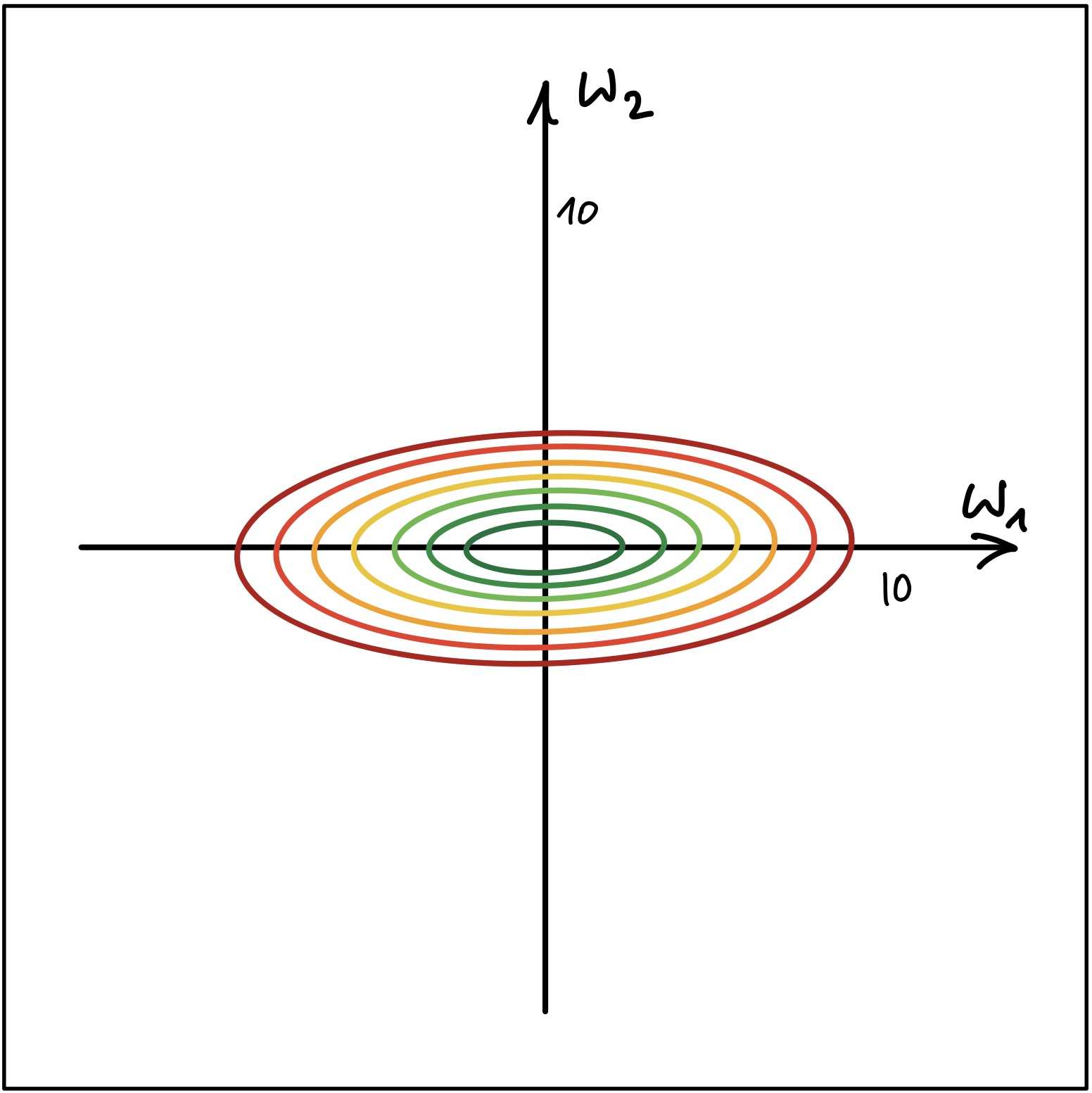
Abbildung 2
- Erklären Sie, welcher der beiden Fälle nachteilhaft für den Gradientenabstieg Algorithmus ist. Wo liegt der Nachteil? Wie kann die Merkmalskalierung dem genannten Nachteil entgegenwirken?
- Zeigen Sie unter Verwendung Ihrer eigenen, zufällig generierten Datenpunkte aus dem Bereich

