Übungsblatt: Overfitting & MLP
(10 Punkte)
NN.MLP.01: Perzeptron-Netze (2P)
Konstruieren Sie ein Netz mit drei Perzeptrons, welches für zwei Eingabevariablen
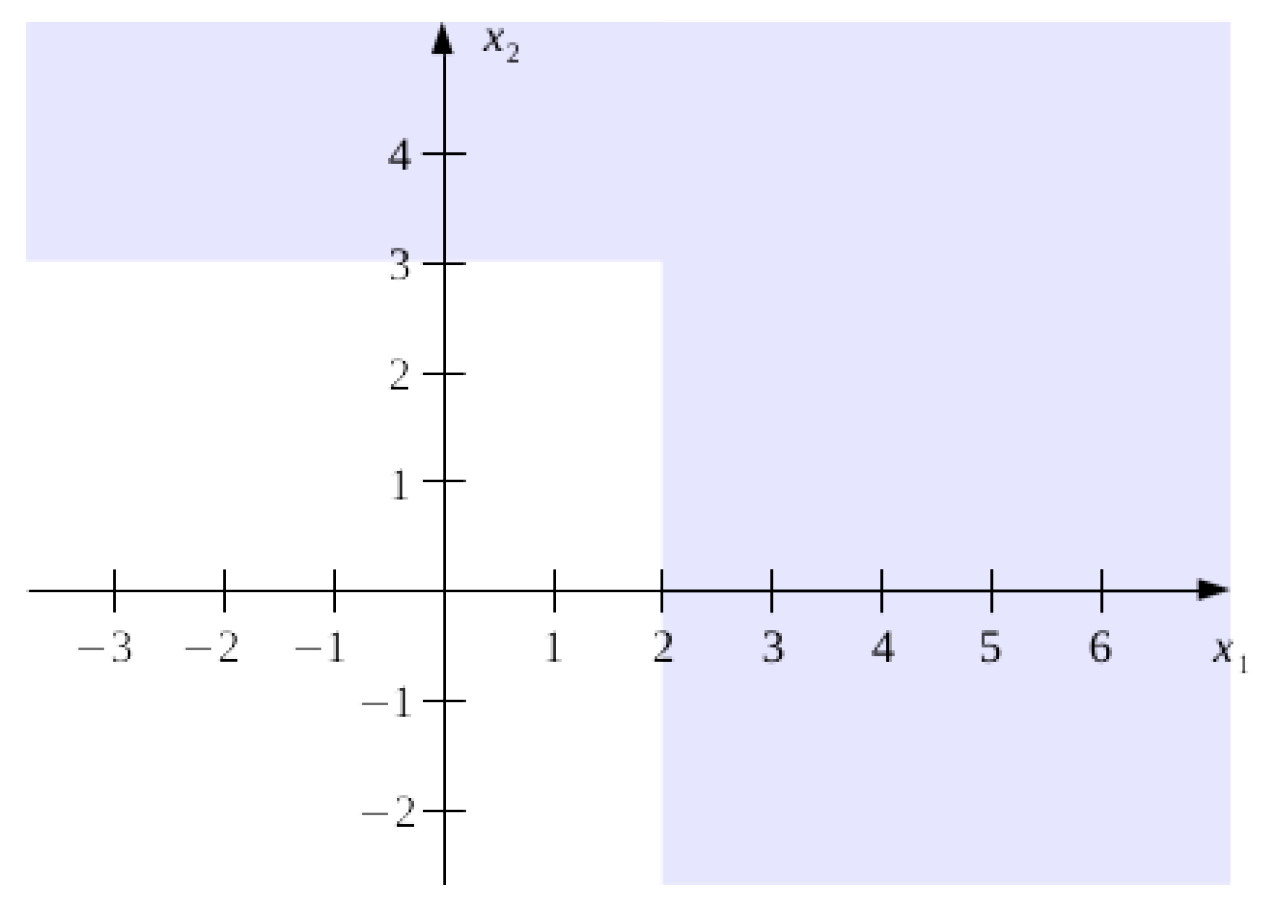
Abbildung 1
NN.MLP.02: Vorwärtslauf im MLP (2P)
Gegeben sei ein MLP mit 25 Zellen in der Eingangsschicht, 64 Zellen in der ersten versteckten Schicht, 32 Zellen in der zweiten versteckten Schicht und 4 Zellen in der Ausgabeschicht (die Bias-Zellen nicht mitgezählt). In allen Zellen wird die ReLU Aktivierungsfunktion verwendet.
- Was sind die Dimensionen der Gewichtsmatrizen
- Wie wird die Ausgabe berechnet? Schreiben Sie den Vorwärtslauf in Matrix-Notation auf. Wie könnte man die Ausgabe deuten; welches Problem könnte durch dieses Netzwerk möglicherweise gelöst werden?
NN.MLP.03: Tensorflow Playground (6P)
Benutzen Sie den Neural Network Playground, um die unten gelisteten Experimente durchzuführen. Achten Sie bei allen Experimenten auf das Verhalten der Trainings- und Testkosten. Sie können mit Hilfe der Checkbox unter der Ausgabezelle (ganz rechts, unten) die Testdaten ein- und ausblenden. Der Play-Knopf startet dabei das Training und der Reload-Knopf setzt das Netzwerk zurück.
-
(1P) Trainieren Sie ein logistisches Regressionsmodell zunächst auf dem "Gaussian" Datensatz (linear separierbarer Datensatz links-unten), danach auf den anderen Datensätzen.
-
(3P) Trainieren Sie ein MLP mit
- einer versteckten Schicht mit 2 Neuronen,
- einer versteckten Schicht mit 3 Neuronen,
- einer versteckten Schicht mit 5 Neuronen,
- zwei versteckten Schichten mit jeweils 5 Neuronen pro Schicht
- drei versteckten Schichten mit jeweils 7 Neuronen pro Schicht
- vier versteckten Schichten mit jeweils 7 Neuronen pro Schicht
auf dem kreisförmigen (Circle) und auf dem spiralförmigen (Spiral) Datensatz, mehrmals mit jeweils den Aktivierungsfunktionen ReLU, tanh und Sigmoid. Hat die Auswahl der Aktivierungsfunktion einen Einfluss auf die Form der Entscheidungsgrenze oder die Geschwindigkeit der Berechnung?
-
(2P) Setzen Sie nun den Noise-Level auf 15 und wiederholen Sie die Experimente. Wann kann von einer Überanpassung gesprochen werden?
Sprechen Sie für alle Experimente die folgenden Punkte an:
- Wie verhält sich die Entscheidungsgrenze?
- Was können Sie über Trainings- und Testkosten sagen? Entsteht eine Überanpassung?
- Wie schnell wird die Entscheidungsgrenze berechnet?
- Können alle Datenpunkte jedes mal korrekt klassifiziert werden? Warum?
- Untersuchen und vergleichen Sie die Ausgaben der Zellen in den versteckten Schichten, in dem Sie die Maus über die jeweilige Zelle bewegen. Bemerken Sie einen wesentlichen Unterschied in den Ausgaben der ersten Schicht im Vergleich zu der letzten Schicht?