MIF 1.5 (PO23): Concepts of Programming Languages (Winter 2024/25)
Kursbeschreibung
Der Compiler ist das wichtigste Werkzeug in der Informatik. In der Königsdisziplin der Informatik schließt sich der Kreis, hier kommen die unterschiedlichen Algorithmen und Datenstrukturen und Programmiersprachenkonzepte zur Anwendung.
In diesem Modul geht es um ein fortgeschrittenes Verständnis für interessante Konzepte im Compilerbau sowie um grundlegende Konzepte von Programmiersprachen und -paradigmen. Wir schauen uns dazu relevante aktuelle Tools und Frameworks an und setzen diese bei der Erstellung eines Bytecode-Compilers für unterschiedliche Programmiersprachen für die Java-VM oder WASM ein.
Überblick Modulinhalte
- Lexikalische Analyse: Scanner/Lexer
- Reguläre Sprachen
- Klassisches Vorgehen: RegExp nach NFA (Thompson's Construction), NFA nach DFA (Subset Construction), DFA nach Minimal DFA (Hopcroft's Algorithm)
- Manuelle Implementierung, Generierung mit ANTLR oder Flex
- Syntaxanalyse: Parser
- Kontextfreie Grammatiken (CFG), Chomsky
- LL-Parser (Top-Down-Parser)
- FIRST, FOLLOW
- Tabellenbasierte Verfahren, rekursiver Abstieg
- LL(1), LL(k), LL(*)
- Umgang mit Vorrang-Regeln, Assoziativität und linksrekursiven Grammatiken
- LR-Parser (Bottom-Up-Parser)
- Shift-Reduce
- LR(0), SLR(1), LR(1), LALR
- Generierung mit ANTLR oder Bison
- Semantische Analyse und Optimierungen
- Symboltabellen
- Namen und Scopes
- Typen, Klassen, Polymorphie
- Attributierte Grammatiken: L-attributed vs. R-attributed grammars
- Typen, Typ-Inferenz, Type Checking
- Datenfluss- und Kontrollfluss-Analyse
- Optimierungen: Peephole u.a.
- Symboltabellen
- Zwischencode: Intermediate Representation (IR), LLVM-IR
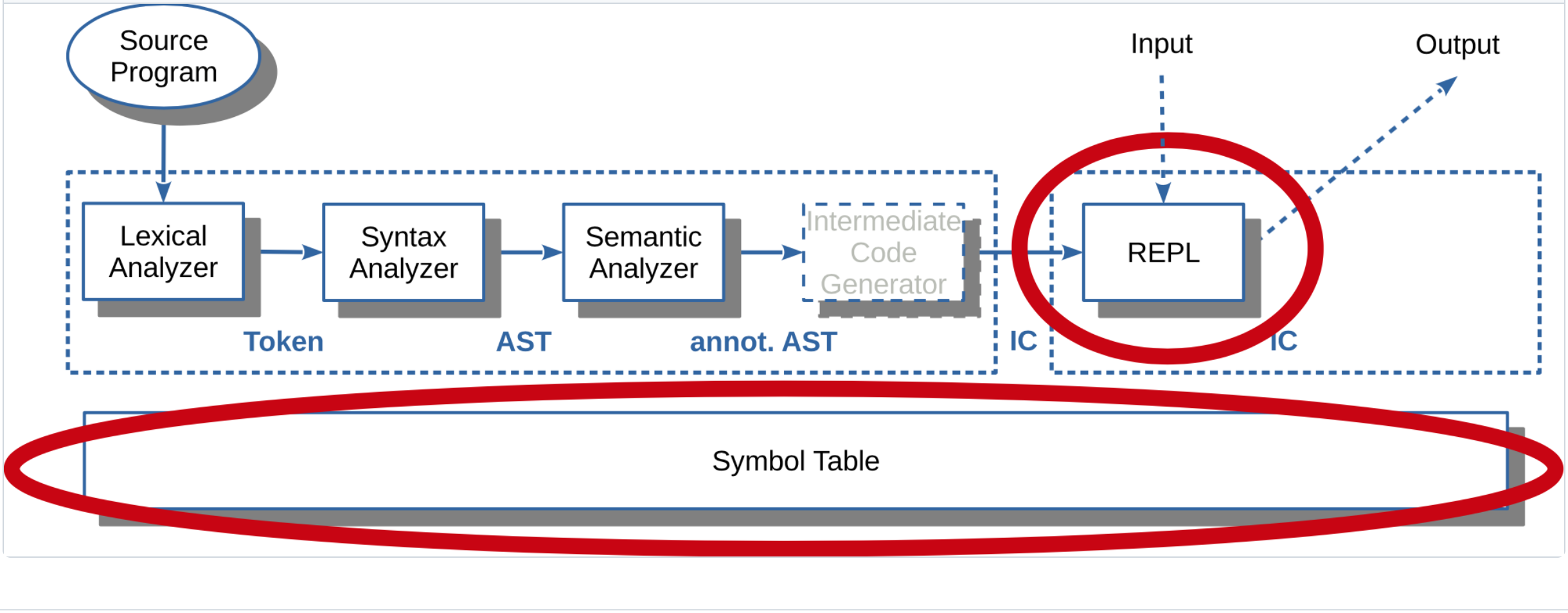
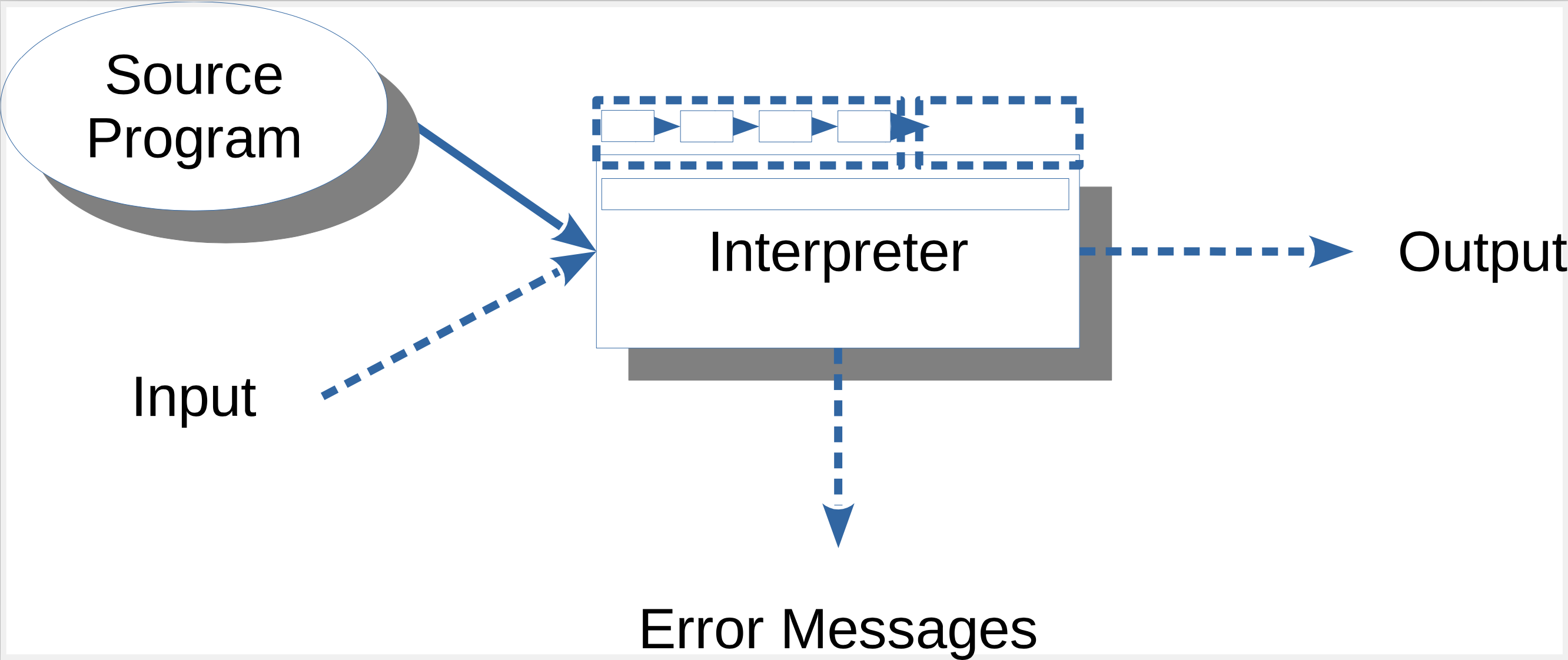
- Interpreter
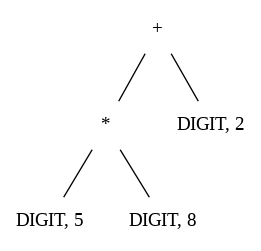
- AST-Traversierung
- Read-Eval-Schleife
- Resolver: Beschleunigung der Interpretation
- Code-Generierung, Bytecode/VM
- Speicherlayout
- Erzeugen von Bytecode
- Ausführen in einer Virtuellen Maschine
- Garbage Collection
- Programmiersprachen: Ruby, Prolog, Haskell, Lisp und die Auswirkungen der Konzepte auf den Compiler/Interpreter und die Laufzeitumgebung
Team
- BC George
- Carsten Gips (Sprechstunde nach Vereinbarung)
Kursformat
| Vorlesung (2 SWS) | Praktikum (3 SWS) |
|---|---|
| Di, 14:00 - 15:30 Uhr (online) | Di, 15:45 - 18:00 Uhr (online) |
| (Carsten: Flipped Classroom, BC: Vorlesung) |
Online-Sitzungen per Zoom (Zugangsdaten siehe ILIAS). Sie können hierzu den Raum J101 (siehe Stundenplan) nutzen.
Fahrplan
Hier finden Sie einen abonnierbaren Google Kalender mit allen Terminen der Veranstaltung zum Einbinden in Ihre Kalender-App.
Abgabe der Übungsblätter jeweils Dienstag bis 14:00 Uhr im ILIAS. Vorstellung der Lösung im jeweiligen Praktikum in der Abgabewoche.
| Monat | Tag | Vorlesung | Lead | Praktikum |
|---|---|---|---|---|
| Oktober | 08. | Orga (Zoom); Überblick, Sprachen, Anwendungen | Carsten, BC | |
| 15. | Reguläre Sprachen, CFG, LL-Parser | BC | Verteilung Themen | |
| 22. | LR-Parser | BC | Status Workshop I | |
| 29. | Workshop I: Sprache und Features (auf Sprachebene) | |||
| 29. | 18:00 - 19:30 Uhr (online): Edmonton I: ANTLR + Live-Coding | Edmonton | ||
| November | 05. | Attributierte Grammatiken | BC | Status Workshop II |
| 12. | Überblick Symboltabellen, Symboltabellen: Scopes, Symboltabellen: Funktionen, Symboltabellen: Klassen | Carsten | Status Workshop II | |
| 19. | Start 15:30 Uhr: Syntaxgesteuerte Interpreter, AST-basierte Interpreter 1, AST-basierte Interpreter 2 | Carsten | Status Workshop II | |
| 26. | 18:00 - 19:30 Uhr (online): Edmonton II: Vorträge Mindener Projekte: Workshop II: Sprache und Features (aus Compiler-Sicht) | Minden (MIF) | ||
| Dezember | 03. | Optimierung und Datenfluss- und Kontrollflussanalyse | BC | |
| Dezember | 03. | 18:00 - 19:30 Uhr (online): Edmonton III: Vorträge Edmontoner Projekte | Edmonton | |
| 10. | Projekt-Pitch: Vorstellen und Diskussion der Projektinhalte/-konzepte | Carsten | ||
| 17. | Freies Arbeiten | Status Workshop III | ||
| 24. | Weihnachtspause | |||
| 31. | Weihnachtspause | |||
| Januar | 07. | Freies Arbeiten | Status Workshop III | |
| 14. | Freies Arbeiten | Status Workshop III | ||
| 21. | Freies Arbeiten | Status Workshop III | ||
| (Prüfungsphase I) | 31. | Workshop III: Projektvorstellung/-übergabe (10:00 - 12:30 Uhr, online) | ||
| (Prüfungsphase I) | 07. | Feedback-Gespräche (10:00 - 12:00 Uhr, online) | ||
| (Prüfungsphase II) | Keine separate Prüfung |
Prüfungsform, Note und Credits
Parcoursprüfung plus Testat, 10 ECTS (PO23)
-
Testat: Vergabe der Credit-Points
- Aktive Teilnahme an mind. 5 der 7 "Status Workshop"-Termine, und
- aktive Teilnahme an allen 3 Edmonton-Terminen.
-
Gesamtnote:
Die Workshops werden bewertet und ergeben in folgender Gewichtung die Gesamtnote:
- 20% Workshop I,
- 30% Workshop II,
- 50% Workshop III.
Die Bearbeitung der Aufgaben (Workshops) erfolgt in 2er Teams.
Materialien
- "Compilers: Principles, Techniques, and Tools". Aho, A. V. und Lam, M. S. und Sethi, R. und Ullman, J. D. and Bansal, S., Pearson India, 2023. ISBN 978-9-3570-5488-1. Online über die O'Reilly-Lernplattform.
- "Crafting Interpreters". Nystrom, R., Genever Benning, 2021. ISBN 978-0-9905829-3-9. Online.
- "Engineering a Compiler". Torczon, L. und Cooper, K., Morgan Kaufmann, 2012. ISBN 978-0-1208-8478-0. Online über die O'Reilly-Lernplattform.
- "Introduction to Compilers and Language Design". Thain, D., 2023. ISBN 979-8-655-18026-0. Online.
- "Writing a C Compiler". Sandler, N., No Starch Press, 2024. ISBN 978-1-0981-8222-9. Online über die O'Reilly-Lernplattform.
- "Seven Languages in Seven Weeks". Tate, B.A., Pragmatic Bookshelf, 2010. ISBN 978-1-93435-659-3. Online über die O'Reilly-Lernplattform.
Förderungen und Kooperationen
Kooperation mit University of Alberta, Edmonton (Kanada)
Über das Projekt "We CAN virtuOWL" der Fachhochschule Bielefeld ist im Frühjahr 2021 eine Kooperation mit der University of Alberta (Edmonton/Alberta, Kanada) im Modul "Compilerbau" gestartet.
Wir freuen uns, auch in diesem Semester wieder drei gemeinsame Sitzungen für beide Hochschulen anbieten zu können. (Diese Termine werden in englischer Sprache durchgeführt.)