Typen, Type Checking und Attributierte Grammatiken
Motivation
Ist das alles erlaubt?
Operation erlaubt?
Zuweisung erlaubt?
Welcher Ausdruck hat welchen Typ?
(Welcher Code muss dafür erzeugt werden?)
- a = b
- a = f(b)
- a = b + c
- a = b + o.nummer
- if (f(a) == f(b))
Taschenrechner: Parsen von Ausdrücken wie 3*5+4
expr : expr '+' term
| term
;
term : term '*' DIGIT
| DIGIT
;
DIGIT : [0-9] ;
=> Wie den Ausdruck ausrechnen?
Anmerkung: Heute geht es um die einfachste Form der semantischen Analyse: Anreichern einer Grammatik um Attribute und Aktionen, die während des Parsens oder bei der Traversierung des Parse-Trees ausgewertet werden.
Semantische Analyse
Das haben wir bis jetzt
Wir haben den AST vorliegen.
Idealerweise enthält er bei jedem Bezeichner einen Verweis in sogenannte Symboltabellen (siehe spätere Veranstaltung).
Was kann beim Parsen schon überprüft / bestimmt werden?
Hier entsteht ein Tafelbild.
Was fehlt jetzt noch?
Kontextsensitive Analysen
Hier entsteht ein Tafelbild.
Analyse von Datentypen
Typisierung
-
stark oder statisch typisierte Sprachen: Alle oder fast alle Typüberprüfungen finden in der semantischen Analyse statt (C, C++, Java)
-
schwach oder dynamisch typisierte Sprachen: Alle oder fast alle Typüberprüfungen finden zur Laufzeit statt (Python, Lisp, Perl)
-
untypisierte Sprachen: keinerlei Typüberprüfungen (Maschinensprache)
Ausdrücke
Jetzt muss für jeden Ausdruck im weitesten Sinne sein Typ bestimmt werden.
Ausdrücke können hier sein:
-
rechte Seiten von Zuweisungen
-
linke Seiten von Zuweisungen
-
Funktions- und Methodenaufrufe
-
jeder einzelne aktuelle Parameter in Funktions- und Methodenaufrufen
-
Bedingungen in Kontrollstrukturen
Typinferenz
Def.: Typinferenz ist die Bestimmung des Datentyps jedes Bezeichners und jedes Ausdrucks im Code.
-
Die Typen von Unterausdrücken bestimmen den Typ eines Ausdrucks
-
Kalkül mit sog. Inferenzregeln der Form
$$\frac{f:s \rightarrow t\ \ \ \ \ x:s}{f(x) : t}$$(Wenn f den Typ $s \rightarrow t$ hat und x den Typ s, dann hat der Ausdruck f(x) den Typ t.)
-
z. B. zur Auflösung von Überladung und Polymorphie zur Laufzeit
Statische Typprüfungen
Bsp.: Der + - Operator:
| Typ 1. Operand | Typ 2. Operand | Ergebnistyp |
|---|---|---|
| int | int | int |
| float | float | float |
| int | float | float |
| float | int | float |
| string | string | string |
Typkonvertierungen
-
Der Compiler kann implizite Typkonvertierungen vornehmen, um einen Ausdruck zu verifizieren (siehe Sprachdefiniton)
-
Typerweiterungen, z.B. von int nach float oder
-
Bestimmung des kleinsten umschließenden Typ vorliegender Typen
-
Type Casts: explizite Typkonvertiereungen
Nicht grundsätzlich statisch mögliche Typprüfungen
Bsp.: Der ^-Operator $(a^b)$:
| Typ 1. Operand | Typ 2. Operand | Ergebnistyp |
|---|---|---|
| int | int $\geq$ 0 | int |
| int | int < 0 | float |
| int | float | float |
| $\ldots$ | $\ldots$ | $\ldots$ |
Attributierte Grammatiken
Was man damit macht
Die Syntaxanalyse kann keine kontextsensitiven Analysen durchführen
-
Kontextsensitive Grammatiken benutzen: Laufzeitprobleme, das Parsen von cs-Grammatiken ist PSPACE-complete
-
Parsergenerator Bison: generiert LALR(1)-Parser, aber auch sog. Generalized LR (GLR) Parser, die bei nichtlösbaren Konflikten in der Grammatik (Reduce/Reduce oder Shift/Reduce) parallel den Input mit jede der Möglichkeiten weiterparsen
-
Anderer Ansatz: Berücksichtigung kontextsensitiver Abhängigkeiten mit Hilfe attributierter Grammatiken, zur Typanalyse, auch zur Codegenerierung
-
Weitergabe von Informationen im Baum
Syntax-gesteuerte Übersetzung: Attribute und Aktionen
Berechnen der Ausdrücke
expr : expr '+' term ;
translate expr ;
translate term ;
handle + ;
Attributierte Grammatiken (SDD)
auch "syntax-directed definition"
Anreichern einer CFG:
-
Zuordnung einer Menge von Attributen zu den Symbolen (Terminal- und Nicht-Terminal-Symbole)
-
Zuordnung einer Menge von semantischen Regeln (Evaluationsregeln) zu den Produktionen
Definition: Attributierte Grammatik
Eine attributierte Grammatik AG = (G,A,R) besteht aus folgenden Komponenten:
-
Mengen A(X) der Attribute eines Nonterminals X
-
G = (N, T, P, S) ist eine cf-Grammatik
-
A = $\bigcup\limits_{X \in (T \cup N)} A(X)$ mit $A(X) \cap A(Y) \neq \emptyset \Rightarrow X = Y$
-
R = $\bigcup\limits_{p \in P} R(p)$ mit $R(p) = \lbrace X_i.a = f(\ldots) \vert p : X_0 \rightarrow X_1 \ldots X_n \in P, X_i.a \in A(X_i), 0 \leq i \leq n\rbrace$
Abgeleitete und ererbte Attribute
Die in einer Produktion p definierten Attribute sind
AF(p) = $\lbrace X_i.a \ \vert\ p : X_0 \rightarrow X_1 \ldots X_n \in P, 0 \leq i \leq n, X_i.a = f(\ldots) \in R(p)\rbrace$
Disjunkte Teilmengen der Attribute: abgeleitete (synthesized) Attributen AS(X) und ererbte (inherited) Attributen AI(X):
-
AS(X) = $\lbrace X.a\ \vert \ \exists p : X \rightarrow X_1 \ldots X_n \in P, X.a \in AF(p)\rbrace$
-
AI(X) = $\lbrace X.a\ \vert \ \exists q : Y \rightarrow uXv \in P, X.a\in AF(q)\rbrace$
Abgeleitete Attribute geben Informationen von unten nach oben weiter, geerbte von oben nach unten.
Abhängigkeitsgraphen stellen die Abhängigkeiten der Attribute dar.
Beispiel: Attributgrammatiken
| Produktion | Semantische Regel |
|---|---|
e : e1 '+' t ; |
e.val = e1.val + t.val |
e : t ; |
e.val = t.val |
t : t1 '*' D ; |
t.val = t1.val * D.lexval |
t : D ; |
t.val = D.lexval |
| Produktion | Semantische Regel |
|---|---|
t : D t' ; |
t'.inh = D.lexval |
t.syn = t'.syn |
|
t' : '*' D t'1 ; |
t'1.inh = t'.inh * D.lexval |
t'.syn = t'1.syn |
|
t' : $\epsilon$ ; |
t'.syn = t'.inh |
Wenn ein Nichtterminal mehr als einmal in einer Produktion vorkommt, werden die Vorkommen nummeriert. (t, t1; t', t'1)
S-Attributgrammatiken und L-Attributgrammatiken
S-Attributgrammatiken
S-Attributgrammatiken: Grammatiken mit nur abgeleiteten Attributen, lassen sich während des Parsens mit LR-Parsern beim Reduzieren berechnen (Tiefensuche mit Postorder-Evaluation):
def visit(N):
for each child C of N (from left to right):
visit(C)
eval(N) # evaluate attributes of NL-Attributgrammatiken
-
Grammatiken, deren geerbte Atribute nur von einem Elternknoten oder einem linken Geschwisterknoten abhängig sind
-
können während des Parsens mit LL-Parsern berechnet werden
-
alle Kanten im Abhängigkeitsgraphen gehen nur von links nach rechts
-
ein Links-Nach-Rechts-Durchlauf ist ausreichend
-
S-attributierte SDD sind eine Teilmenge von L-attributierten SDD
Beispiel: S-Attributgrammatik
| Produktion | Semantische Regel |
|---|---|
e : e1 '+' t ; |
e.val = e1.val + t.val |
e : t ; |
e.val = t.val |
t : t1 '*' D ; |
t.val = t1.val * D.lexval |
t : D ; |
t.val = D.lexval |
Beispiel: Annotierter Syntaxbaum für 5*8+2

Annotierter Parse-Tree
Erzeugung des AST aus dem Parse-Tree für 5*8+2
| Produktion | Semantische Regel |
|---|---|
e : e1 '+' t ; |
e.node = new Node('+', e1.node, t.node) |
e : t ; |
e.node = t.node |
t : t1 '*' D ; |
t.node = new Node('*', t1.node, new Leaf(D, D.lexval)); |
t : D ; |
t.node = new Leaf(D, D.lexval); |
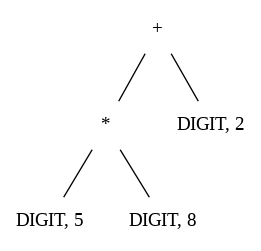
AST
Beispiel: L-Attributgrammatik, berechnete u. geerbte Attribute, ohne Links-Rekursion
Teil der vorigen SDD zum Parsen und Berechnen von Ausdrücken wie 5*8+2, hier umformuliert ohne Links-Rekursion
und mit berechneten und geerbten Attributen:
| Produktion | Semantische Regel |
|---|---|
t : D t' ; |
t'.inh = D.lexval |
t.syn = t'.syn |
|
t' : '*' D t'1 ; |
t'1.inh = t'.inh * D.lexval |
t'.syn = t'1.syn |
|
t' : $\epsilon$ ; |
t'.syn = t'.inh |
5*8 =>

Annotierter Parse-Tree mit berechneten und geerbten Attributen (nur Multiplikation)
Vorgriff: Dies ist ein Beispiel für eine "L-attributierte SDD".
Beispiel: Typinferenz für 3+7+9 oder "hello"+"world"
| Produktion | Semantische Regel |
|---|---|
e : e1 '+' t ; |
e.type = f(e1.type, t.type) |
e : t ; |
e.type = t.type |
t : NUM ; |
t.type = "int" |
t : NAME ; |
t.type = "string" |
Syntax-gesteuerte Übersetzung (SDT)
Erweiterung attributierter Grammatiken
Syntax-directed translation scheme:
Zu den Attributen kommen Semantische Aktionen: Code-Fragmente als zusätzliche Knoten im Parse Tree an beliebigen Stellen in einer Produktion, die, wenn möglich, während des Parsens, ansonsten in weiteren Baumdurchläufen ausgeführt werden.
e : e1 {print e1.val;}
'+' {print "+";}
t {e.val = e1.val + t.val; print(e.val);}
;
S-attributierte SDD, LR-Grammatik: Bottom-Up-Parsierbar
Die Aktionen werden am Ende jeder Produktion eingefügt ("postfix SDT").
| Produktion | Semantische Regel |
|---|---|
e : e1 '+' t ; |
e.val = e1.val + t.val |
e : t ; |
e.val = t.val |
t : t1 '*' D ; |
t.val = t1.val * D.lexval |
t : D ; |
t.val = D.lexval |
e : e1 '+' t {e.val = e1.val + t.val; print(e.val);} ;
e : t {e.val = t.val;} ;
t : t1 '*' D {t.val = t1.val * D.lexval;} ;
t : D {t.val = D.lexval;} ;
L-attributierte SDD, LL-Grammatik: top-down-parsebar (1/2)
| Produktion | Semantische Regel |
|---|---|
t : D t' ; |
t'.inh = D.lexval |
t.syn = t'.syn |
|
t' : '*' D t'1 ; |
t'1.inh = t'.inh * D.lexval |
t'.syn = t'1.syn |
|
t' : $\epsilon$ ; |
t'.syn = t'.inh |
t : D {t'.inh = D.lexval;} t' {t.syn = t'.syn;} ;
t' : '*' D {t'1.inh = t'.inh * D.lexval;} t'1 {t'.syn = t'1.syn;} ;
t' : e {t'.syn = t'.inh;} ;
L-attributierte SDD, LL-Grammatik: Top-Down-Parsierbar (2/2)
-
LL-Grammatik: Jede L-attributierte SDD direkt während des Top-Down-Parsens implementierbar/berechenbar
-
SDT dazu:
-
Aktionen, die ein berechnetes Attribut des Kopfes einer Produktion berechnen, an das Ende der Produktion anfügen
-
Aktionen, die geerbte Attribute für ein Nicht-Terminalsymbol $A$ berechnen, direkt vor dem Auftreten von $A$ im Körper der Produktion eingefügen
-
Implementierung im rekursiven Abstieg
Implementierung im rekursiven Abstieg
-
Geerbte Attribute sind Parameter für die Funktionen für die Nicht-Terminalsymbole
-
berechnete Attribute sind Rückgabewerte dieser Funktionen.
T t'(T inh) {
match('*');
T t1inh = inh * match(D);
return t'(t1inh);
}Wrap-Up
Wrap-Up
-
Die Typinferenz benötigt Informationen aus der Symboltabelle
-
Einfache semantische Analyse: Attribute und semantische Regeln (SDD)
-
Umsetzung mit SDT: Attribute und eingebettete Aktionen
-
Reihenfolge der Auswertung u.U. schwierig
Bestimmte SDT-Klassen können direkt beim Parsing abgearbeitet werden:
-
S-attributierte SDD, LR-Grammatik: bottom-up-parsebar
-
L-attributierte SDD, LL-Grammatik: top-down-parsebar
Ansonsten werden die Attribute und eingebetteten Aktionen in den Parse-Tree, bzw. AST, integriert und bei einer (späteren) Traversierung abgearbeitet.
-
- [Aho2023] Compilers: Principles, Techniques, and Tools, Updated 2nd Edition by Pearson
Aho, A. V. und Lam, M. S. und Sethi, R. und Ullman, J. D. und Bansal, S., Pearson India, 2023. ISBN 978-9-3570-5488-1.
Kapitel 2.3 und 5 - [Levine2009] flex & bison
Levine, J., O'Reilly, 2009. ISBN 978-0-5961-5597-1.
- (K2) Konzept der attributierten Grammatiken: Anreicherung mit Attributen und semantischen Regeln
- (K2) Unterschied zwischen geerbten und berechneten Attributen
- (K2) Umsetzung von SDD mit Hilfe von SDT
- (K3) Einfache semantische Analyse mit Hilfe von attributierten Grammatiken