Übungsblatt: Backpropagation
(10 Punkte)
NN.Backprop.01: Gewichtsupdates für versteckte Schichten (2P)
In der Vorlesung wurde(n) die Gewichtsupdates bei der Backpropagation für die Ausgabeschicht und die davor liegende letzte versteckte Schicht hergeleitet, wobei in der Ausgabeschicht die Sigmoid und in der versteckten Schicht die ReLU Aktivierungsfunktionen eingesetzt wurden. Leiten Sie die Gewichtsupdates für die erste versteckte Schicht (für ein Netz mit zwei echten versteckten Schichten) her. Verwenden Sie dabei die Sigmoid Funktion als Aktivierung in allen Schichten.
Thema: Verständnis Backpropagation
NN.Backprop.02: Forward- und Backpropagation (2P)
Betrachten Sie das folgende MLP mit zwei Schichten mit insgesamt zwei Zellen. Die Gewichte sind an den Kanten angegeben. Das Netz erhält den skalaren Input $x$ und berechnet daraus die Ausgabe $y$. Beide Zellen verwenden die Aktivierungsfunktion $\sigma(z) = \frac{1}{ 1 + e^{−z} }$.
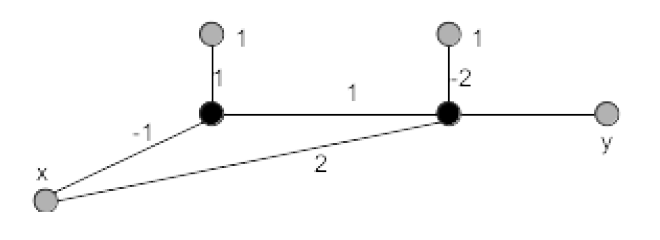
Abbildung 1
-
(1P) Berechnen Sie die Ausgabe $y$ für die Eingabe $(x,y_T)=(0, 0.5)$. Wie groß ist der Fehler?
-
(1P) Berechnen Sie die partiellen Ableitungen für die Gewichte. Wie lauten die Gewichtsupdates für das obige Trainingsbeispiel? Setzen Sie $\alpha = 0.01$.
NN.Backprop.03: MLP und Backpropagation (6P)
Implementieren Sie ein Feedforward MLP mit mindestens einer versteckten Schicht. Nutzen Sie die Cross-Entropy Verlustfunktion.
-
(2P) Implementieren Sie die Forwärtspropagation. Nutzen Sie als Aktivierungsfunktion in der Ausgangsschicht $g(z) = \frac{1}{ 1 + e^{−z} }$ und in der versteckten Schicht $g(z) = ReLU(z)$.
-
(2P) Implementieren Sie das Backpropagations-Verfahren zum Aktualisieren der Gewichte. Achten Sie insbesondere darauf, die bereits berechneten partiellen Ableitungen der jeweils hinteren Schicht wieder zu verwenden (und nicht jeweils erneut zu berechnen!), d.h. propagieren Sie die Fehler von hinten nach vorn durch das Netz.
-
(2P) Trainieren Sie das Netz für den Iris-Datensatz (iris.csv) aus dem AIMA-Repository und nutzen Sie dabei die Variante des stochastischen Gradientenabstiegs. Messen Sie pro Epoche (also nach jedem Durchlauf durch den kompletten Datensatz) den Trainingsfehler. Zeichnen Sie den Trainingsfehler als Diagramm über den Epochen auf.
Falls der Trainingsfehler nach einigen tausend Epochen nicht gegen einen Wert nahe Null strebt, erweitern Sie Ihr Netz (beispielsweise eine versteckte Schicht mehr oder mehr Zellen in der schon existierenden versteckten Schicht, ...) und trainieren Sie es erneut. Nach wievielen Epochen ist der Trainingsfehler fast Null?
Thema: Verständnis MLP und Backpropagation, Gefühl für nötige Größe des Netzes